It's based on a Penrose tiling, which is an aperiodic tiling derived from tiling pentagons. (I'll let wikipedia explain it).
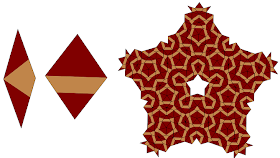
I used a combination of machine piecing and English paper piecing to construct it using two types of diamonds:
and I lay them out in this base tiling:
Then I do two tricky things that exploit some of the niftier properties of Penrose tilings: matching rules and inflation/deflation. These need to be explained in more detail...
Constructing Penrose Tiling using Matching Rules
These rhombi (plural of rhombus, a fancy word for diamond) can be tiled in a lot of ways that are not actually Penrose tilings. They can be tiled in ways that are periodic, or completely non-periodic:
and you can certainly make some lovely quilts doing this:
 |
| This was made by Domesticat |
 |
| This was made by Dorothea |
My first plan was to design a quilt that copied the curved design as shown in the above diagram (but just the pink lines):
NOTE: Penrose tiling is beyond the powers of Electric Quilt, so I designed these using Geometer's Sketchpad instead.
I made this pot holder as a test to see if it was feasible to make the entire full sized quilt this way:
Although this was strictly feasible, I found that all the curved lines and sharp points made this too tricky for my skill level.
So I decided to tweak the matching rules into straight lines:
This way I can machine piece these straight lines first and paper piece the rhombi.
Constructing Penrose Tiling using Inflation/Deflation Properties
One of the mind-bending properties of a Penrose tiling is that if all the rhombi in a given tiling are broken up like so:
The resulting tiling is also a Penrose tiling of smaller tiles. In this example I deflate this simple tiling one level:
Now I can deflate this tiling down another level (I shaded a couple of rhombi from the previous level to illustrate this):
You can continue this indefinitely. Here's 3 and 4 level deflation:
The flip side of this is inflation; any tiling can be combined into larger tiles by reversing this process. So any tiling, no matter how large, is only a subset of a single rhombus (mind = blown).
This inspired me to design a quilt that exploits this property. I first thought it would be interesting to have a quilt that uses different sized rhombi:
Then I thought it would be cool if I designed a quilt where all the rhombi were the same size, but by using different colors and/or values (light and dark), an inflated level of Penrose tiling would emerge:
The combination of this design with the matching rule design above became the final design for the Christmas tree skirt:

















I know I must read this a number of times before I really understand this, but your explanations, and especially the examples, the one with large and small on the same quilt helped my brain to capture the meaning.(I can tell) It will take a while, and more readings, playing with the concepts, before my brain can help me understand. magnificent work. very inspiring. Thank you. I am not even a quilter, but now think I might venture forth. Ginny
ReplyDeleteI know I must read this a number of times before I really understand this, but your explanations, and especially the examples, the one with large and small on the same quilt helped my brain to capture the meaning.(I can tell) It will take a while, and more readings, playing with the concepts, before my brain can help me understand. magnificent work. very inspiring. Thank you. I am not even a quilter, but now think I might venture forth. Ginny
ReplyDelete